問1:T君は午前8時に家を出発し、10km離れた学校との間を時速3kmで往復し続けます。
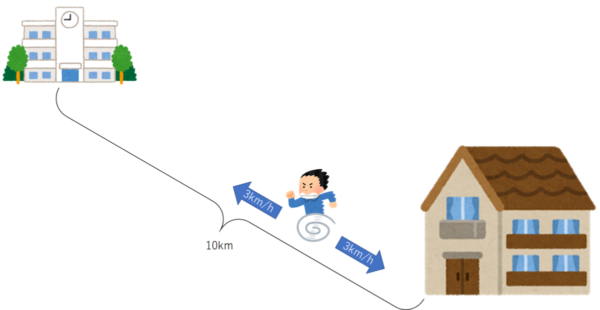
T君がこのような行動をとる理由を答えよ。
こんにちは、チオールです。
皆さんは数学の問題を解くときに、「この登場人物は何でこんなことをしているのだろう?」と疑問に思ったことはありませんか。
そういった「奇行問題(登場人物の変な行動が描写される問題)」の多くは、数学世界のものを我々人間の住む下界へと無理矢理引きずり降ろそうとした結果生じるものです。我々の日常と縁のない、難しい概念の問題であればあるほど、その奇行度は増していきます。

ということは、国際数学オリンピック(IMO)で出るような超難問には、教科書では見られないようなブッ飛んだ奇行が見られるのではないでしょうか。
※国際数学オリンピック(International Math Olympiad):毎年行われる高校生を対象とした数学の問題を解く能力を競う国際大会。略称は"IMO"。
というわけで、この記事では国際数学オリンピックの奇行問題のうち特にブッ飛んでいた4問を紹介します。
絶交イベント
まず最初に紹介するのは、2019年の問題3です。
あるソーシャルネットワークサービスにはユーザーが2019人おり、そのうちのどの2人も互いに友人であるか互いに友人でないかのどちらかである。いま、次のようなイベントが繰り返し起きることを考える:
3人のユーザーA、B、Cの組であって、AとB、AとCが友人であり、BとCは友人でないようなものについて、BとCが友人になり、AはB、Cのどちらとも友人ではなくなる。これら以外の2人組については変化しないとする。───
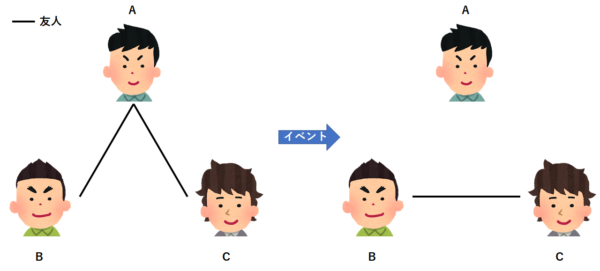
何だそのイベント?
ここでいう「イベント」とは大きな催し物等のことではなく、単に「出来事」という意味の単語だと思われますが、それにしても内容が不可解です。
「友達二人から縁を切られたうえで、その二人が友達関係になる」という出来事がどのような理由で起きるのかはわかりませんが、それを考えるとどうしても "裏切り" という言葉が脳内にチラついてきます。
そして、問題の続きがこちら。
───はじめに、友人の数が1009人であるユーザーが1010人、友人の数が1010人であるユーザーが1009人存在するとする。上のようなイベントが何回か起きた後、全てのユーザーの友人の数が高々1人になることがあることを示せ。
悲惨すぎる。
ユーザーの総数は2019人なので、「友人の数が1009人であるユーザーが1010人、友人の数が1010人であるユーザーが1009人存在する」ということは全てのユーザーが他の全ユーザーの半数と友人であるということになります。
そんな親密なコミュニティに対して、一体どんな大事件が起きれば「全員の友人の数が1人以下」なんてことになるのでしょうか。もはや全く想像できません。
見えないうさぎ
次は2017年の問題3です。
ハンターと見えないうさぎが平面上でゲームを行う。───
いきなり謎のワードが出てきました。
「見えないうさぎ」って何?
───うさぎが最初にいる点A0とハンターが最初にいる点B0は一致している。n−1回のラウンドが終わった後、うさぎは点An−1におり、ハンターはBn−1にいる。n回目のラウンドにおいて、次の3つが順に行われる:
(i) うさぎはAn−1からの距離がちょうど1であるような点Anに見えないまま移動する。
(ii) 追跡装置がある点Pnをハンターに知らせる。ただし、PnとAnの距離が1以下であるということだけが保証されている。
(iii) ハンターは Bn−1からの距離がちょうど1であるような点Bnに周りから見えるように移動する。───
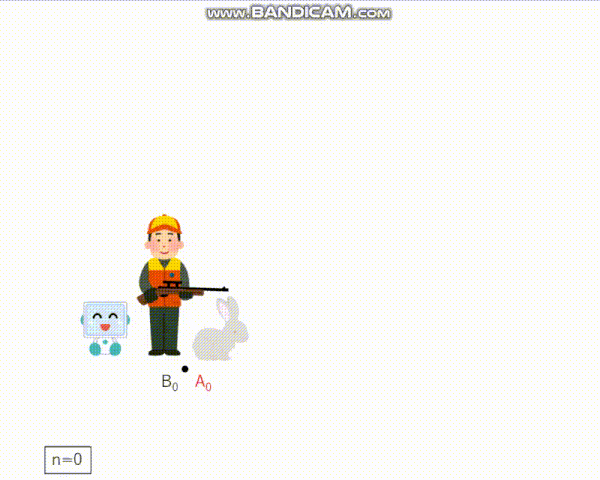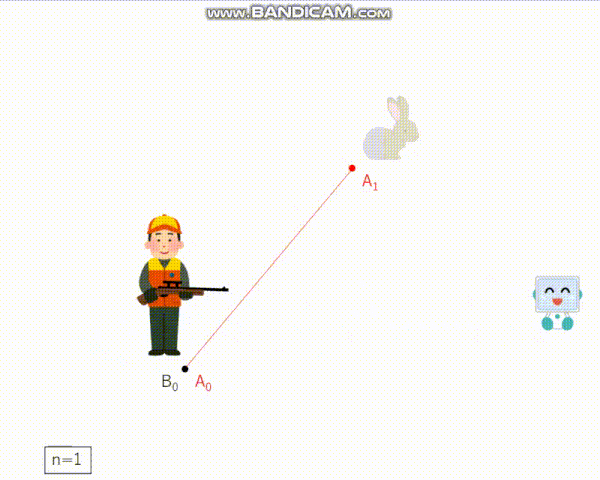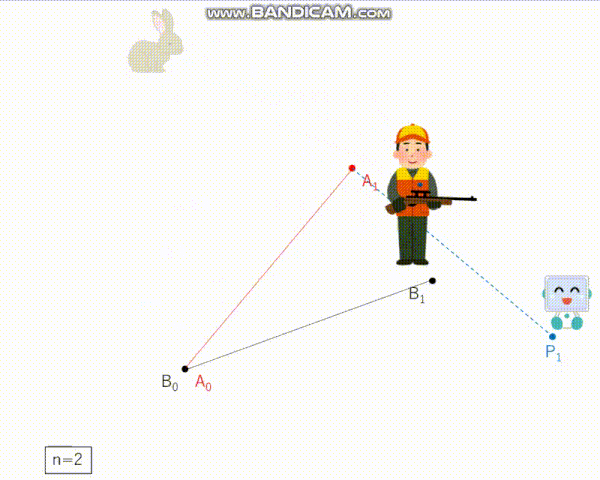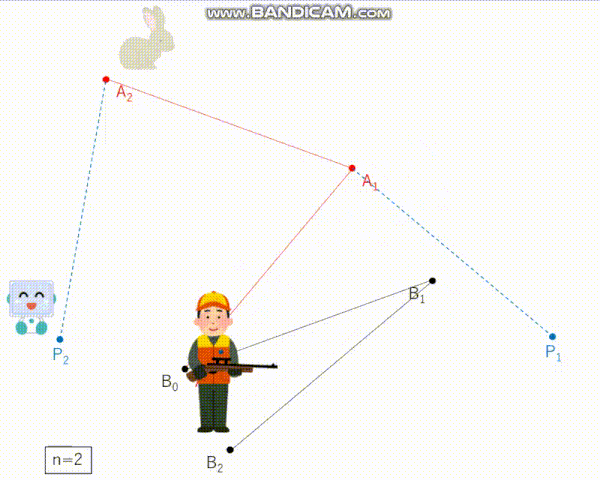
どうやらこの問題は、ハンターが「追跡装置」なるものを使用して見えないうさぎと追いかけっこをする、という設定のようです。
それにしても、やはり「見えないうさぎ」という概念が謎ですね。
ハンターの妄想か何かかと思ったんですが、追跡装置で捕捉できるということは確かにその場にいるのかもしれません。
───うさぎがどのように移動するかにかかわらず、またどの点が追跡装置によって知らされるかにかかわらず、ハンターは 109回のラウンドが終わった後に必ずうさぎとの距離を100以下にすることができるか。
長くない?
仮に1ラウンドが1秒で終わるとしても、109ラウンドが終わるまでに約31年かかります。
長くない???
31年間、追跡装置の「ここから距離1以内にいる」という不確かな情報だけを頼りに見えないうさぎを追うハンターは何を思うのでしょうか。
何が彼を駆り立てるのでしょうか。それとも、何かの罰なのでしょうか。
ところで、ふと気になってググってみたところ、
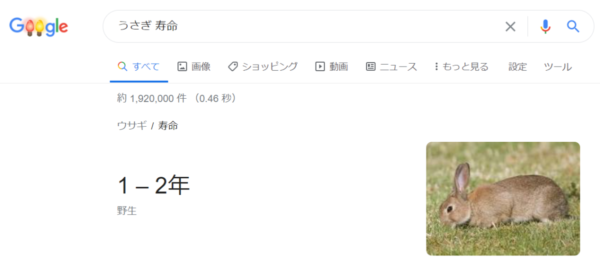
うさぎの寿命は1~2年だそうです。
……やっぱり全部ハンターの妄想で、見えないうさぎなんてものは最初から存在しないのでは?
「通常の8~31倍ほど長命で、さらに不可視であるようなうさぎが存在する」という解釈と「不可視のうさぎがいると信じ込み、31年間追跡し続けている人物がいる」という解釈、果たしてどちらの方が「現実的」でしょうか。
コインと箱と、あと宇宙
続いて紹介するのは、2010年の問題5。
6つの箱B1、B2、B3、B4、B5、B6があり、コインが1枚ずつ入っている。次の2種類の操作を考える。:
- 操作1:空でない箱Bj(1≤j≤5)を選び、箱Bjからコインを1枚取り除き、箱Bj+1に2枚のコインを入れる。
- 操作2:空でない箱Bj(1≤k≤4)を選び、箱Bkからコインを1枚取り除き、箱Bk+1と箱Bk+2の中身を入れ替える(ただし、これらの箱は空であってもよい)。───
箱の中身を出し入れするだけの地味~なゲームに見えますが、箱の中身が「コイン」となると金銭の授受のにおいがしてきます。
例えば「ゲーム終了時に箱に残っていたコインの枚数に応じて賞金がもらえる」というルールだと、単なる奇行ではなくちゃんとしたゲームのようにも思えてきますね。まぁそんなこと書いてませんが。
問題は以下のように続きます。
───これらの操作を有限回行い、箱B1、B2、B3、B4、B5が空かつ箱B6にちょうど201020102010個のコインが入っているようにできるか。ただし、abcはa(bc)を表すものとする。
多い。明らかに多い。
もしコイン1個が1円玉だったとしても、箱に残る金額は201020102010円です。5000兆円どころの騒ぎではありません。
例えば我々の住む宇宙に存在する素粒子(物質を構成する最小単位の粒子)の個数は多めに見積もっても1090個程度らしく、201020102010個はそれよりも異次元に多いです。
どうやら、このゲームをやるには随分と大きな宇宙が必要となります。
ちなみに、このゲームにおいてB6に残せるコインの個数には上限があるらしいのですが、実はその個数は201020102010個よりかなり多いみたいです。
実際に筆者が計算してみたところ……
1010101010. . .10
(10が10101010101010101010個)個を超えるっぽいです。
怖。
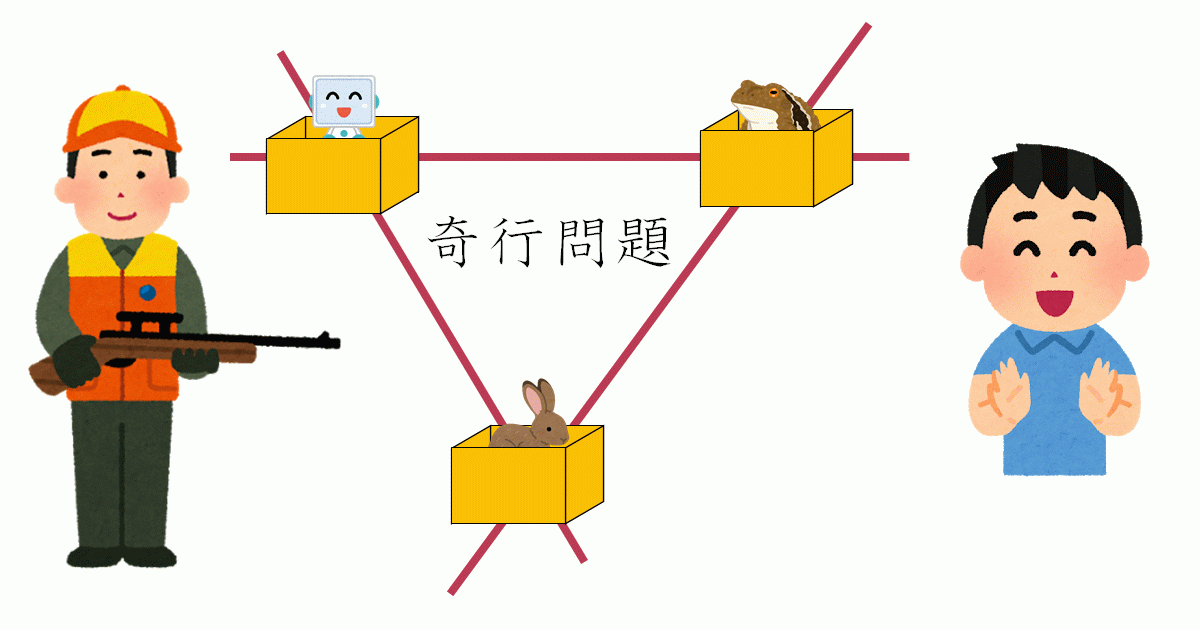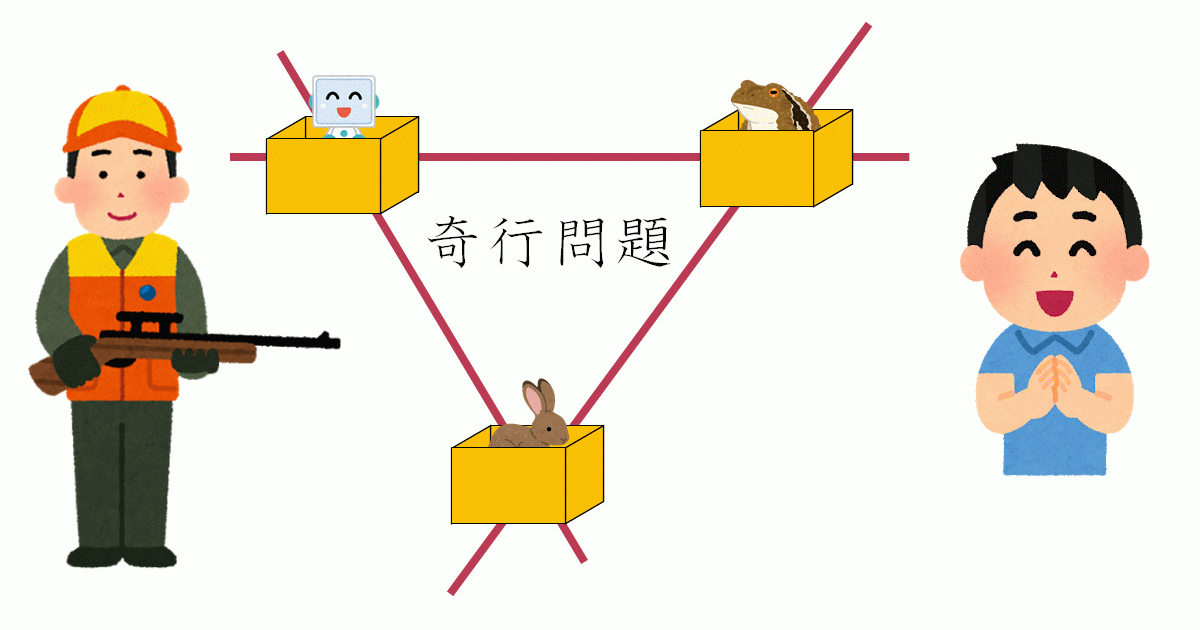
カエルマスター 晋一
最後は、2016年の第6問です。
nを2以上の整数とする。平面上にn本の線分があり、どの2本も端点以外で交点をもち、どの3本も1点で交わらないとする。───
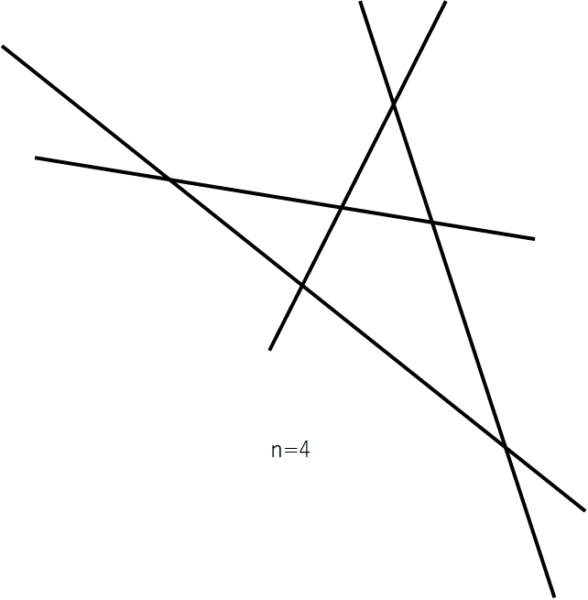
───晋一君はそれぞれの線分についていずれかの端点を選び、もう片方の端点を向くように1匹ずつカエルを配置する。───
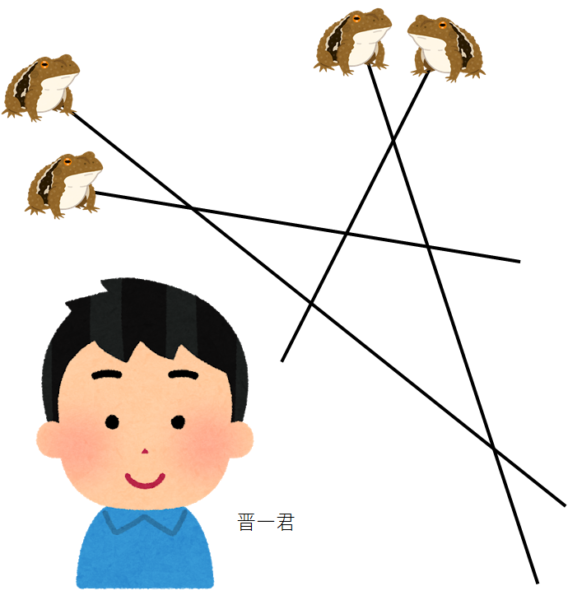
───次に、晋一君はn−1回手をたたく。 晋一君が1回手をたたくごとに、それぞれのカエルは線分上の隣の交点に跳び移る。ただしそれぞれのカエルは移動する向きを変えないとする。晋一君の目標はうまくカエルを配置することで、どの2匹のカエルも同時に同じ点にいることがないようにすることである。

まず、晋一君が平然とカエルを操っていることが目を引きます。
手を叩くことでカエルを移動させていることから「音で驚かせて飛び跳ねさせているだけでは?」と思うかもしれませんが、そう上手くいくとは思えません。
図を描いてみるとわかるのですが、問題で指定された条件の線分における交点間の距離(=カエルの飛び跳ねる距離)は、線分の本数が多いとバラバラになります。
ということは、カエルのジャンプ力を一回ずつ・一匹ずつ調整しなければ隣の交点に着地させられません。
また、大量のカエルを同一平面上に配置するとなると、カエル同士の相互作用(縄張り争いとか)も発生するはずです。
これらの要素を完璧に制御する方法としては、以下のようなものが考えられます。
- カエルを躾ける
(高度な調教技術が必要) - 平面上に餌や何らかの化学物質を配置し、カエルの動きを制御する
(カエルの生体的特性についての知見が必要) - 魔法的な何かを使う
(魔法的な何かが必要)
いずれにせよ、晋一君は只者ではないでしょう。
話は変わりますが、実はnが奇数のとき、以下のような星形の配置が条件を満たします。
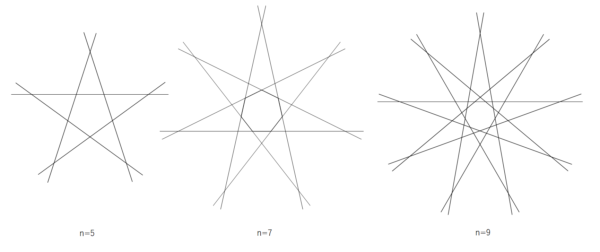
また、問題には以下のような続きがあります。
(a) nが奇数のとき、晋一君は必ず目標を達成できることを示せ。
(b) nが偶数のとき、晋一君は決して目標を達成できないことを示せ。
つまり、nが奇数のときは線分を星形に配置することができ、その上でカエルをうまく移動させることが必ずできるということになります。
これらを合わせて考えることで、晋一君の奇行に隠された意図が見えてきます。
ずばり、晋一君が行おうとしているのは黒魔術の儀式ではないでしょうか?
n本の線分が魔法陣の役割を果たし、その上でカエルたちが舞い踊ることにより何らかの超常的な効果を発動させようとしているのではないでしょうか。
また、先述の「晋一君が平然とカエルを操ってるの変じゃね?」という話も、「そういう世界観だから」の一言で片づけられます。
最後に
最初に説明したとおり、この記事は数学教育や作問者への批判的意図を一切含まないので、各方面に対して極力失礼のない表現を選んで書いています。
……と思っていたんですが、よく考えると現実の矮小な宇宙や人間関係と比べたり、挙句の果てに妄想やら黒魔術と紐付けたりしていて数学そのものに対して失礼ですね。
というわけで、数学神の怒りを買った私は10kmの直線上を時速3kmで往復し続ける罰を受けなければならないので、この辺で失礼します。
それでは、さようなら。
記事冒頭 問1の解答例:罰
(執筆:チオール)
読了おめでとう!次はこちらの記事をどうぞ!








 年間人気記事ランキング2025
年間人気記事ランキング2025 年間人気記事ランキング2024
年間人気記事ランキング2024 年間人気記事ランキング2023
年間人気記事ランキング2023 年間人気記事ランキング2022
年間人気記事ランキング2022 年間人気記事ランキング2021
年間人気記事ランキング2021 年間人気記事ランキング2020
年間人気記事ランキング2020 年間人気記事ランキング2019
年間人気記事ランキング2019 年間人気記事ランキング2018
年間人気記事ランキング2018 エッッッッッッッ記事王決定戦
エッッッッッッッ記事王決定戦 狂気記事王決定戦
狂気記事王決定戦 こたつ記事王決定戦
こたつ記事王決定戦